
CONCURSO PÚBLICO SARGENTE DO EXÉRCITO BRASILEIRO: SAIU O EDITAL
RESUMO DO CONCURSO PÚBLICO:
SARGENTO EXÉRCITO BRASILEIRO | ESA
- Órgão: Exército Brasileiro
- Cargo: Sargento do Exército
- Escolaridade: Nível médio
- Idade: 17 a 24 anos.
- Altura: Mínimo 1,60 m para homens e 1,55 m para mulheres.
- Número de vagas: 1.100 VAGAS | 900 Masculino (Área Geral), sendo 180 destinadas à cota de negros. 100 Feminino (Área Geral), 20 sendo à cota de negros.
- Remuneração: Durante o curso de formação recebe um auxilio maior que R$ 1.000, ao final do curso (3º sargento) R$ 3.825,00
- Banca: Comissão Própria
- Isenção de Matricula: de 07 a 09 de Abril (no site da ESA)
- Inscrições: de 07 de Abril a 04 de Maio (no site da ESA)
- Valor da Inscrição: R$ 95,00 (noventa e cinco reais)
- Formato da Prova: Múltipla Escolha
- Prova Dissertativa (REDAÇÃO): Sim
- Quantidade de Redações a Serem Corrigidas: 3.850 (três mil oitocentos e cinquenta).
- Teste de Aptidão Física: Sim
LOCAL DE REALIZAÇÃO DAS PROVAS: Brasil inteiro (As cidades podem ser consultados no Edital)
Data da prova: 03 de Outubro de 2021
VOCÊ SABE COMO FUNCIONA UM CONCURSO PÚBLICO?
O concurso público é um processo pra selecionar pessoas para trabalhar no governo, ou seja, se tornarem servidores públicos.
Esse processo de Seleção tem início com a realização de uma PROVA OBJETIVA + REDAÇÃO, que servem para selecionar os melhores candidatos.
Após ser aprovado nessa etapa o candidato passa por outras fases como: Exames Médicos e o Teste Físico.
O candidato sendo Aprovado em todas essas etapas descritas anteriormente, se torna um servidor público (começa a Trabalhar para o Governo).
Conteúdo da Prova: Objetiva + Redação
Prova Objetiva:
A Prova Objetiva será composta de 40 questões de múltipla escolha, referente ao Ensino Médio, com 5 alternativas de respostas para cada questão, sendo apenas uma alternativa correta.
Contém os seguintes conteúdos descritos abaixo com os respectivo numero de questões e com os pesos descritos abaixo:

Redação:
A parte discursiva de Português, de caráter eliminatório, será constituída de uma redação e terá o objetivo de avaliar a capacidade de expressão escrita e o uso das normas do registro formal culto da Língua Portuguesa. O candidato deverá produzir, com base no tema indicado na questão discursiva, uma redação com extensão mínima de 20 (vinte) e máxima de 30 (trinta) linhas, sem contar o título, primando pela coerência, correção e coesão. Será distribuída ao candidato uma folha de rascunho para que, caso assim deseje, possa fazer anotações, organizar suas ideias e/ou elaborar o esboço de sua redação. Contudo, tal rascunho deverá ser passado a limpo na Folha de Redação e à caneta. Somente o texto produzido na Folha de Redação será corrigido.
Critérios para que devem ser observados para evitar zerar a Redação:

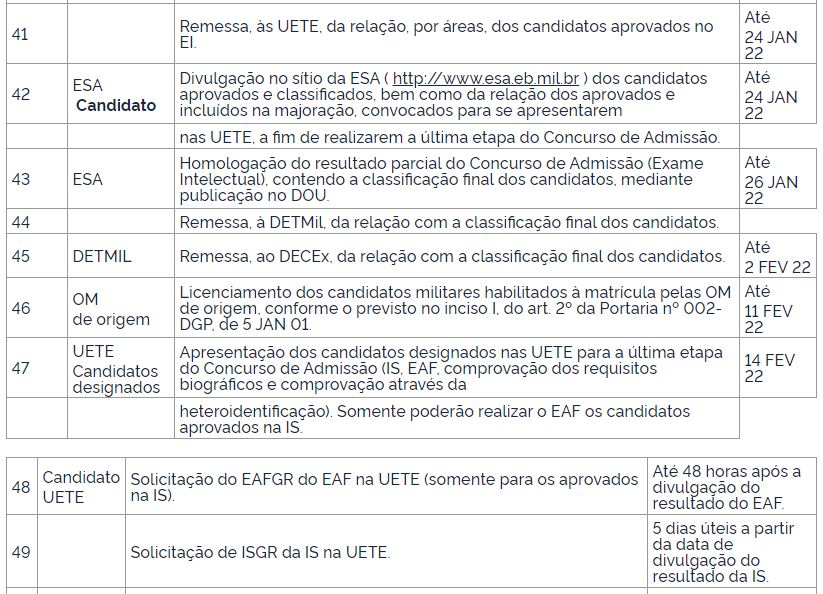
Calendário de Atividades:






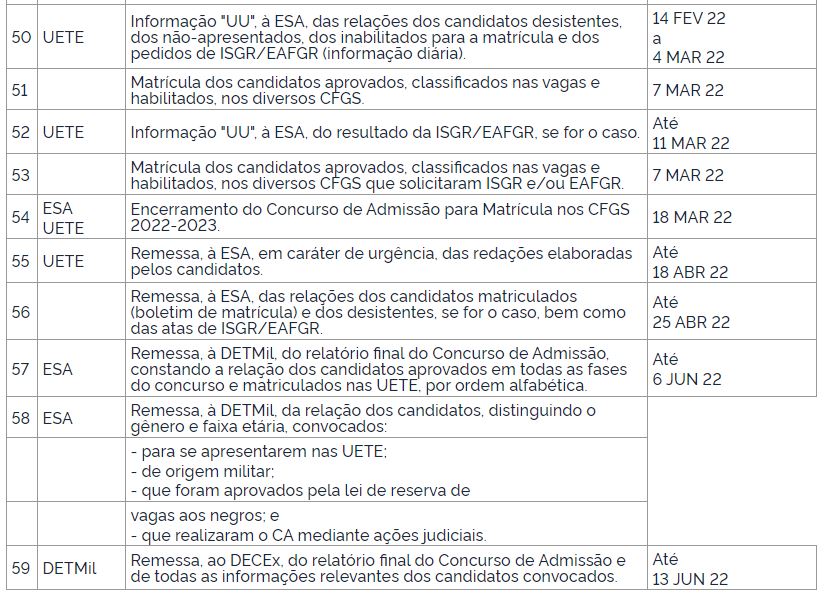
Inspeção de Saúde:
O candidato convocado deverá comparecer ao local determinado pela UETE (Unidade Escolar Tecnológica do Exército), portando documento de identificação, e apresentará sua caderneta de vacinação, se a possuir. Terá, ainda, que apresentar, obrigatoriamente, os laudos dos exames complementares, abaixo relacionados, cuja realização é de sua responsabilidade, com os respectivos resultados:
I – radiografia dos campos pleuro-pulmonares (com laudo);
II – sorologia para Lues (método de VDRL) e HIV;
III – exame de detecção de Doença de Chagas, utilizando um dos métodos a seguir: hemoaglutinação; imunofluorescência; ELISA (ou imunoensaio enzimático) ou reação de Machado-Guerreiro;
IV – hemograma completo, tipagem sanguínea e fator RH, e coagulograma;
V – parasitologia de fezes;
VI – sumário de urina (EAS, urina tipo I ou urina rotina);
VII – teste ergométrico (com laudo);
VIII – eletroencefalograma em vigília com mapeamento (com laudo);
IX – radiografia panorâmica das arcadas dentárias (com laudo);
X – audiometria (tonal, com laudo);
XI – sorologia para hepatite B (contendo, no mínimo, HBsAg e Anti-HBc) e hepatite C (Anti-HCV);
XII – exame oftalmológico (com laudo, incluindo motilidade; acuidade visual; fundoscopia; tonometria; teste de Ishiara, relatando quais a cores em déficit);
XIII – glicemia em jejum;
XIV – uréia e creatinina;
XV – colesterol frações, triglicerídeo e ácido úrico;
XVI – TSH, T4 e T3;
XVII – radiografia de coluna cervical, torácica (realizadas em 2 incidências: PA e Perfil) e lombar com LAUDO, ESPECIFICANDO OS ÂNGULOS DE COBB E FERGUSON;
XVIII – exame toxicológico, baseado em matriz biológica (queratina, cabelo ou pelo) com janela de detecção mínima de 90 dias (com laudo). Deverá apresentar resultados negativos para um período superior a 30 (trinta) dias e inferior a 90 (noventa) dias (com laudo). As drogas a serem pesquisadas serão, no mínimo, maconha e derivados; cocaína e derivados – incluindo crack e merla; anfetaminas; metanfetaminas; ecstasy (MDMA e MDA); opiáceos, incluindo morfina, codeína, 6-acetilmorfina (heroína), oxicodine; hidromorfina, hidrocodona;
XIX – teste de gravidez beta-HCG sanguíneo (sexo feminino); e
XX – colpocitologia oncótica (sexo feminino).
Parágrafo único. No caso de impedimento anatômico para ser submetida ao Exame Citopatológico Ginecológico (Preventivo do Câncer Ginecológico), a candidata, obrigatoriamente deverá apresentar atestado médico, emitido por ginecologista, constatando o motivo do impedimento e declarando a ausência de restrições ginecológicas para a participação da candidata no processo seletivo.
Exame de Aptidão Física:
I – abdominal supra (para ambos os sexos):
a) tempo máximo de 3 (três) minutos;
II – flexão de braços sobre o solo (para ambos os sexos):
a) sem limite de tempo;
III – corrida de 12 (doze) minutos (para ambos os sexos):
a) execução: partindo da posição inicial de pé, o candidato deverá correr ou andar a distância que conseguir, no tempo de 12 minutos, podendo interromper ou modificar seu ritmo;
IV – flexão de braços na barra fixa (para ambos os sexos):
a) tempo máximo de 3 (três) minutos;
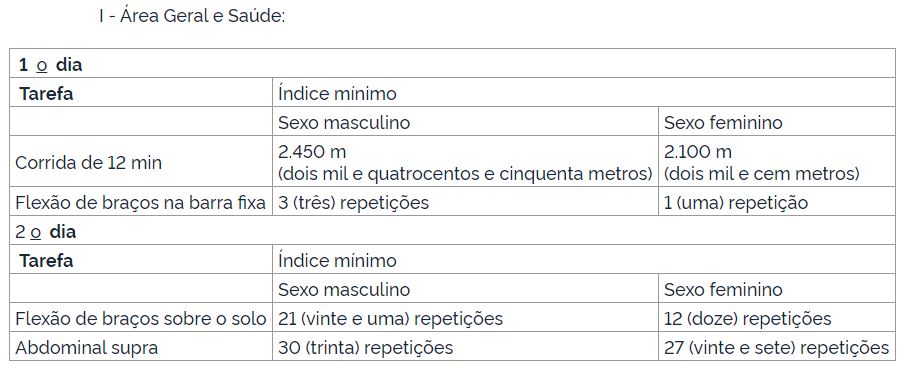
As tarefas serão realizadas em dois dias consecutivos, e os candidatos deverão atingir os seguintes índices mínimos para aprovação, conforme Tabela a seguir:
CONHEÇA UMA HISTÓRIA DE SUCESSO: APROVADO NA ESA
ENTRE EM NOSSO GRUPO EXCLUSIVO CFO BOMBEIROS MG no WHATSAPP
Clique abaixo para entrar em nosso grupo Exclusivo CFO BOMBEIROS MG no WhatsApp, e se juntar a centenas de outros alunos que também estão se preparando para o concurso.
RELAÇÃO DOS ASSUNTOS DO EXAME INTELECTUAL
MATEMÁTICA
1) Teoria dos Conjuntos e Conjuntos Numéricos
a) representação de conjuntos, subconjuntos, operações: união, interseção, diferença e complementar. Conjunto universo e conjunto vazio;
b) conjunto dos números naturais e inteiros: operações fundamentais, números primos, fatoração, número de divisores, máximo divisor comum e mínimo múltiplo comum;
c) conjunto dos números racionais: operações fundamentais.
d) conjunto dos números reais: operações fundamentais, módulo, representação decimal, operações com intervalos reais. Razões e proporções, grandezas diretamente e indiretamente proporcionais e porcentagem; e
e) números complexos: operações, módulo, conjugado de um número complexo, representações algébrica e trigonométrica. Representação no plano de Argand – Gauss, Potencialização e radiciação. Extração de raízes. Fórmulas de Moivre. Resolução de equações binomiais e trinomiais.
2) Funções
a) definição, domínio, imagem, contradomínio, funções injetoras, sobrejetoras e bijetoras, funções pares e ímpares, funções periódicas; funções compostas;
b) relações;
c) raiz de uma função;
d) função constante, função crescente, função decrescente;
e) função definida por mais de uma sentença; e
f) função inversa e seu gráfico.
3) Função Linear, Função Afim e Função Quadrática
a) gráficos, domínio, imagem e características;
b) variações de sinal;
c) máximos e mínimos; e
d) inequação produto e inequação quociente.
4) Função Modular
a) definição, gráfico, domínio e imagem da função modular;
b) equações modulares; e
c) inequações modulares.
5) Função Exponencial
a) gráficos, domínio, imagem e características da função exponencial, logaritmos decimais; e
b) equações e inequações exponenciais.
6) Função Logarítmica
a) definição de logaritmo e propriedades operatórias;
b) gráficos, domínio, imagem e características da função logarítmica; e
c) equações e inequações logarítmicas.
7) Trigonometria
a) arcos notáveis;
b) trigonometria no triângulo (retângulo e qualquer);
c) lei dos senos e lei dos cossenos;
d) unidades de medidas de arcos e ângulos: o grau e o radiano;
e) círculo trigonométrico, razões trigonométricas e redução ao 1º quadrante;
f) funções trigonométricas, transformações, identidades trigonométricas fundamentais, equações e inequações trigonométricas no conjunto dos números reais;
g) fórmulas de adição de arcos, arcos duplos, arco metade e transformação em produto; e
h) sistemas de equações e inequações trigonométricas e resolução de triângulos.
8) Contagem e Análise Combinatória
a) fatorial: definição e operações;
b) princípios multiplicativo e aditivo da contagem;
c) arranjos, combinações e permutações; e
d) binômio de Newton: desenvolvimento, coeficientes binomiais e termo geral.
9) Probabilidade
a) experimento aleatório, experimento amostral, espaço amostral e evento;
b) probabilidade em espaços amostrais equiprováveis;
c) probabilidade da união de dois eventos;
d) probabilidade condicional;
e) propriedades das probabilidades; e
f) probabilidade de dois eventos sucessivos e experimentos binomiais.
10) Matrizes, Determinantes e Sistemas Lineares
a) operações com matrizes (adição, multiplicação por escalar, transposição e produto);
b) matriz inversa;
c) determinante de uma matriz: definição e propriedades; e
d) sistemas de equações lineares.
11) Sequências Numéricas e Progressões
a) sequências numéricas;
b) progressões aritméticas: termo geral, soma dos termos e propriedades; e
c) progressões geométricas (finitas e infinitas): termo geral, soma dos termos e propriedades.
12) Geometria Espacial de Posição
a) posições relativas entre duas retas;
b) posições relativas entre dois planos;
c) posições relativas entre reta e plano;
d) perpendicularidade entre duas retas, entre dois planos e entre reta e plano; e
e) projeção ortogonal.
13) Geometria Espacial Métrica
a) prismas: conceito, elementos, classificação, áreas e volumes e troncos;
b) pirâmide: conceito, elementos, classificação, áreas e volumes e troncos;
c) cilindro: conceito, elementos, classificação, áreas e volumes e troncos;
d) cone: conceito, elementos, classificação, áreas e volumes e troncos;
e) esfera: elementos, seção da esfera, área, volumes e partes da esfera; e
f) inscrição e circunscrição de sólidos.
14) Geometria Analítica Plana
a) ponto: o plano cartesiano, distância entre dois pontos, ponto médio de um segmento e condição de alinhamento de três pontos;
b) reta: equações geral e reduzida, interseção de retas, paralelismo e perpendicularidade, ângulo entre duas retas, distância entre ponto e reta e distância entre duas retas, bissetrizes do ângulo entre duas retas, área de um triângulo e inequações do primeiro grau com duas variáveis;
c) circunferência: equações geral e reduzida, posições relativas entre ponto e circunferência, reta e circunferência e duas circunferências; problemas de tangência; e equações e inequações do segundo grau com duas variáveis;
d) elipse: definição, equação, posições relativas entre ponto e elipse, posições relativas entre reta e elipse;
e) hipérbole: definição, equação da hipérbole, posições relativas entre ponto e hipérbole, posições relativas entre reta e hipérbole e equações das assíntotas da hipérbole;
f) parábola: definição, equação, posições relativas entre ponto e parábola, posições relativas entre reta e parábola; e
g) reconhecimento de cônicas a partir de sua equação geral.
15) Geometria Plana
a) Ângulo: definição, elementos e propriedades;
b) Ângulos na circunferência;
c) Paralelismo e perpendicularidade;
d) Semelhança de triângulos;
e) Pontos notáveis do triângulo;
f) Relações métricas nos triângulos (retângulos e quaisquer);
g) Triângulos retângulos, Teorema de Pitágoras;
h) Congruência de figuras planas;
i) Feixe de retas paralelas e transversais, Teorema de Tales;
j) Teorema das bissetrizes internas e externas de um triângulo;
k) Quadriláteros notáveis;
l) Polígonos, polígonos regulares, circunferências, círculos e seus elementos;
m) Perímetro e área de polígonos, polígonos regulares, circunferências, círculos e seus elementos;
n) Fórmula de Heron;
o) Razão entre áreas; e
p) Inscrição e circunscrição.
16) Polinômios
a) função polinomial, polinômio identicamente nulo, grau de um polinômio, identidade de um polinômio, raiz de um polinômio, operações com polinômios e valor numérico de um polinômio;
b) divisão de polinômios, Teorema do Resto, Teorema de DAlembert e dispositivo de Briot-Ruffini; e
c) relação entre coeficientes e raízes. Fatoração e multiplicidade de raízes e produtos notáveis. Máximo divisor comum de polinômios.
17) Equações Polinomiais
Teorema fundamental da álgebra, teorema da decomposição, raízes imaginárias, raízes racionais, relações de Girard e teorema de Bolzano.
Obs.: Todos os assuntos da Matemática do Ensino Fundamental são pré-requisitos para a prova.
18) Bibliografia sugerida
Constitui apenas uma indicação para elaboração e correção dos itens propostos nas provas do exame intelectual, não esgotando o conteúdo dos assuntos relacionados.
a) DANTE, Luiz Roberto. Matemática: contexto e aplicações. Vol. Único. 4ª edição. Editora Ática, 2011.
b) DANTE, Luiz Roberto. Projeto VOAZ Matemática.Vol. Único, 1ª, 2ª e 3ª Parte. 4ª edição. São Paulo: Ática, 2015 (Coleção Projeto VOAZ).
c) GIOVANNI, José Ruy, BONJORNO, José Roberto e GIOVANNI JR, José Ruy. Matemática Fundamental:Uma Nova Abordagem. Volume único. São Paulo: FTD, 2013.
d) IEZZI, Gelson, DOLCE, Osvaldo, DEGENSZAJN, David, PÉRIGO, Roberto & ALMEIDA, Nilze de. Matemática – Ciências e Aplicações. Volumes 1, 2 e 3. 8ª edição. São Paulo: Atual, 2014.
e) IEZZI, Gelson, ET AL. Fundamentos de Matemática Elementar. Volumes de 1 a 7 e de 9 a 11, Atual Editora, São Paulo, 2006.